并查集

并查集

​ 并查集这一数据结构虽然难度并不大，但是非常重要，在之后的Kruskal算法，LCA等都会用到并查集，顾名思义，并查集就是又并又查又集，那这三个字是什么意思，接下来举个例子更加详细地解释一下。 同学们在学校的时候通常会遇到拉帮结派的现象（不提倡），并查集就实现了每个帮派的分配，并：将两个人合并到一个帮派；查：查找一个人在哪个帮派；集：一个集合，也可以理解成一个帮派。那么通过这个例子我们也就更加直白地理解了并查集是什么东西以及它的作用是什么，接下来就通过具体说明来实现一下并查集的操作

1.合并两个集合

并查集的第一个字就是并（合并），因此合并集合在并查集里是非常重要的一个操作，假设有无同学和他的两个同学羊同学，安同学，我们需要把羊同学和安同学合并到无同学所在的帮派，我们该如何做呢？

在此我们要引入一个新概念，“树”（只是概念）下图便是一个最最最常见的二叉树，我们用此对一些名词概念作解释（图片来源百度）

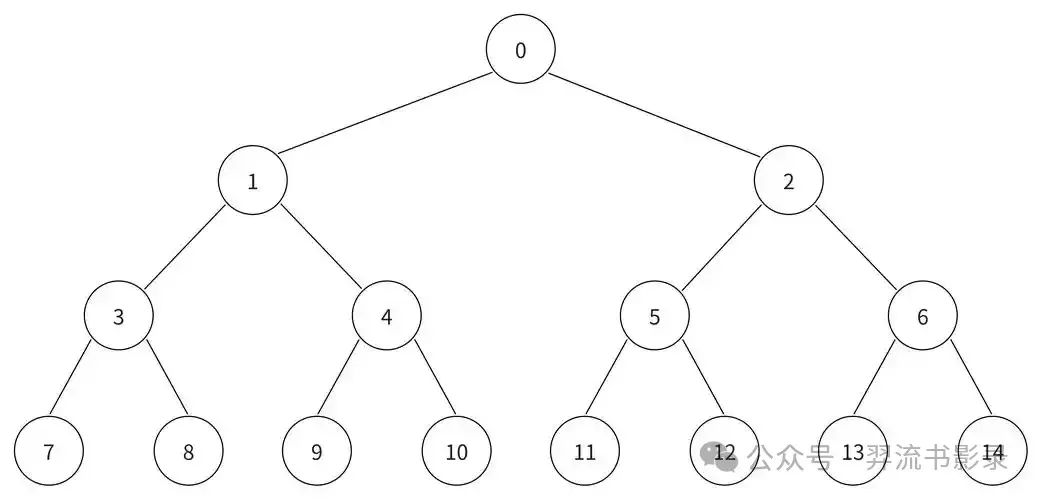
父节点：所有节点都来源于0节点，因此我们将0节点称为父节点，同理，3也是7和8的父节点

子节点：例如1和2就是0的子节点

在并查集中，初始时候每个元素都是单独的一个集合，我们需要通过查找来查找每个集合的代表元素，也可以理解成帮派首领，我们需要查找羊同学和安同学的首领，（为何不用查找无同学的首领，因为他自己就是首领），并且将羊同学和安同学的首领纳入无同学麾下，那么也就实现了几个帮派的合并，当然，在此案例中羊同学和安同学就是他们原来帮派的首领

2.集合的初始化

刚才提到了在最开始要对集合进行初始化，也就是为每个元素分配一个独立的集合，没有交集，因为不好描述因此我们将三个同学换成1，2，3来描述，我们可以用数组s[i]来描述并查集的集，i就是三个同学所代表的元素，初始化非常简单，我们只需要把i赋值给s[i]就大功告成了。

3.集合元素的查询

那么经过了一番折腾，每个帮派的人都发生了天翻地覆的变化，可能羊同学和无同学去了猛虎帮，安同学去了野狼帮，那万一人一多我们该如何查找谁在哪个帮派呢？

刚才我们提到了每个元素都有自己的父节点，也就是各自的首领，我们以无同学举例，假设无同学的父节点是他自己，那么他就是首领，我们也就不需要继续查找，加入首领不是他，那我们只需要递归这个过程，就可以找到无同学的首领，一旦找到首领我们目的也就达到了

说完了这几个操作，并查集还有一个非常重要的操作，路径压缩，我们需要递归查找到根节点，这是一个非常漫长的过程，很有可能导致代码超时，那么路径压缩就避免了这个问题，我们只需要在递归的同时将所有节点设为根节点即可，见下图

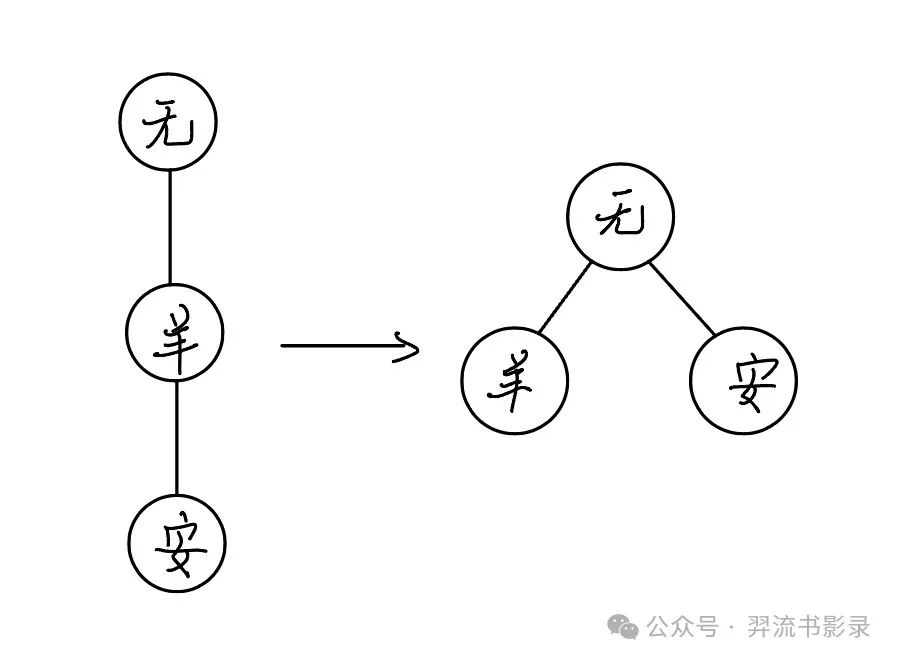
通过这一操作我们便将O(n)的时间复杂度降低到了几乎O(1)

题目

请自行打开链接查看题目（题目太长影响观感）

https://www.luogu.com.cn/problem/P1551

这个题目便是非常经典的并查集模版，因为上述模版已经讲的非常详细，我们直接给出代码，代码中会有一些注释

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 5010;
int father[N]; // 存储父节点

// 初始化
void init(int n) {
    for (int i = 1; i <= n; i++) {
        father[i] = i;
    }
}

// 元素查找
int find(int x) {
    if (x != father[x]) {
        father[x] = find(father[x]);  // 路径压缩
    }
    return father[x];
}

// 合并集合
void merge(int x, int y) {
    x = find(x);
    y = find(y);
    if (x != y) {
        father[x] = y; // 把 y 合并入 x 的集合
    }
}

int main() {
    int n, m, p;
    cin >> n >> m >> p;

    init(n);

    while (m--) {
        int x, y;
        cin >> x >> y;
        merge(x, y);
    }

    while (p--) {
        int x, y;
        cin >> x >> y;
        if (find(x) == find(y)) {
            cout << "Yes" << endl;
        } else {
            cout << "No" << endl;
        }
    }

    return 0;
}

通过此文也相信大家粗略地掌握了并查集的知识，那么留一道刚才题目的加强版本作为思考，题目难度并不大，可以把思路写在评论区下一期进行解析

https://www.luogu.com.cn/problem/P1892

同时也欢迎读者关注我们的公众号